티스토리 뷰
목차
베르누이 법칙의 정의
베르누이 법칙은 유체역학에서 유체의 흐름과 관련된 중요한 원리 중 하나입니다. 이 법칙은 스위스의 수학자 다니엘 베르누이가 1738년에 발표한 '유체역학(Hydrodynamica)'에서 처음 소개되었습니다. 베르누이 법칙은 비압축성 유체(공기나 물과 같이 밀도가 일정한 유체)의 흐름에서 속도가 빨라지면 압력이 낮아진다는 관계를 설명합니다.
베르누이 법칙의 수학적 표현 베르누이 법칙은 다음과 같은 수식으로 표현됩니다.
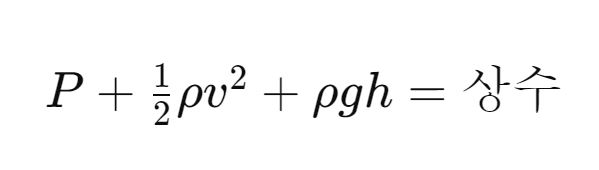
여기서,
- P는 유체의 압력,
- ρ는 유체의 밀도,
- v는 유체의 속도,
- g는 중력 가속도,
- h는 유체의 높이입니다.
이 식은 유체의 어느 지점에서든 압력 에너지, 운동 에너지, 그리고 위치 에너지의 합이 일정하다는 것을 의미합니다.
베르누이 법칙의 응용
항공학: 비행기의 날개는 베르누이 법칙을 이용하여 설계됩니다. 날개의 상부 표면이 하부 표면보다 더 길게 만들어져 있어 유체의 속도를 상부에서 빠르게 하여 압력을 낮춥니다. 이로 인해 상승력이 발생하여 비행기가 하늘을 날 수 있습니다.
환기 시스템: 베르누이 법칙은 공기의 흐름을 통제하여 건물 내부의 환기를 돕습니다. 공기가 좁은 통로를 지날 때 속도가 증가하고 압력이 감소하는 원리를 이용합니다.
자동차: 자동차의 에어 인테이크 시스템과 배기 시스템은 베르누이 법칙을 활용하여 공기 흐름을 최적화합니다. 이는 연료 효율성을 높이고 엔진의 성능을 향상시키는 데 기여합니다.
베르누이 법칙의 한계
베르누이 법칙은 많은 실제 상황에서 유용하지만, 몇 가지 제한이 있습니다. 이 법칙은 비압축성 유체와 정상 흐름에만 적용되며, 점성이 있는 유체나 터뷸런스 흐름에는 별도의 고려가 필요합니다.
결론
베르누이 법칙은 유체역학을 이해하는 데 필수적인 원리로, 다양한 공학적 설계와 기술에 광범위하게 적용됩니다. 이 법칙은 우리가 일상생활에서 사용하는 많은 기기와 시스템의 작동 원리를 이해하는 데 중요한 역할을 합니다. 베르누이 법칙을 통해 유체의 행동을 예측하고 최적화하는 것은 과학과 기술 발전에 있어 핵심적인 요소입니다.
